Binary: representation of signed and unsigned integers

Lesson readings,Website links: Subtraction, multiplication, division, and negative numbers power point slide show
Sample code link:

You have already learned simple binary math, and you also know how unsigned binary numbers are handled. In this lesson, you will learn about signed numbers and how negative numbers are handled. With unsigned numbers, remember all digits may be used to represent the number. When you look at signed numbers, however, this changes. There needs to be some way of determining if a number is negative or positive.

By using a sign-magnitude notation, you can utilize the most significant bit (MSB) as your sign 'flag'. In other words, you give up some values in exchange for the ability to identify a number as positive or negative:

This helps you visualize this process:

So, with this, if we use the MSB as a "sign" bit, with a zero (0) representing a positive number and a one (1) representing a negative number, we have to realize two things immediately:

• No longer does a word represent 256 numbers (0-255). It now represents a maximum of 127.
• The word has a value of -127 to +127.

Now, let's apply this to an actual digit. Positive 53₁₀ looks like this:

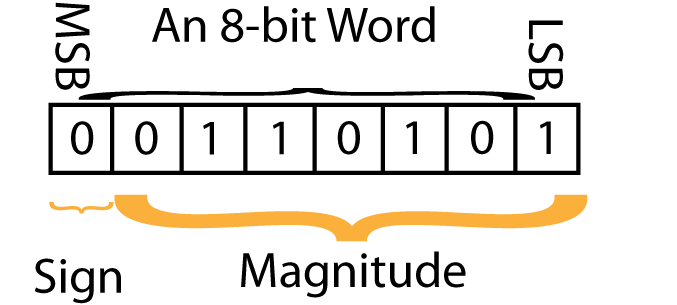
If, on the other hand, you wanted to show a negative (-53), the binary notation would be:

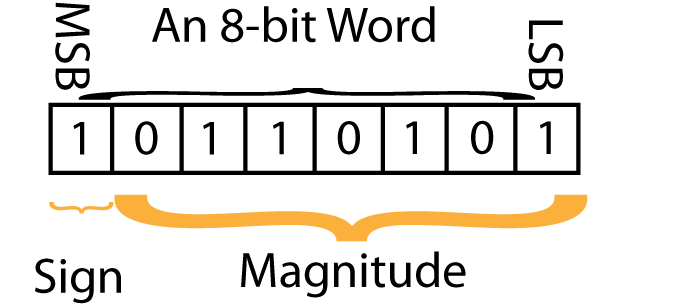
In each case, there are 7 bits available for the number and one bit for the sign. Smaller numbers, such as a 4-bit nibble as well as larger numbers can also be signed or unsigned. These are specific data types that need to be declared when the variables and constants are initialized.

Ones Compliment/Negation

In addition to using the S-M notation, negative numbers can also be represented and manipulated using the Ones Compliment method, also known as negation. Before you pull your hair out at this new 'complication, let's look at how this is managed.

All positive numbers have a MSB of 0. Therefore, all negative numbers will always have a 1 as their MSB. A logic gate (a physical piece of hardware) called an Inverter A logic gate that reverses the state of each bit in the data line: a 1 becomes a zero and a zero becomes a 1. changes each bit in the data line (either a parallel A data flow where each bit flows in either a nibble, word, long word, or other structure all at once. or a Serial Each bit travels in a line, one after the other. data line; you will learn about these later.) to its inverse.

To execute a binary subtraction operation (e.g. "adding" a positive and a negative number), you need to execute an invert on the number to be subtracted. So, if we were subtracting 13 from 54, our numbers would look like:

54₁₀ is 0011 0010₂ and
13₁₀ is 0000 1101₂

To subtract 0000 1101 from 0011 0010, we need to invert the first number (make 0's 1's and 1's 0's):

0011 0010
1111 0010 (now inverted) Now, it's simply adding the numbers (and carrying as needed):

0010 0100 (now add 1)

0010 0101 (1+8+32=41; 54-13=41)

Now before you start looking for the magic wand and the sorcerer's stone, let's look at another example:

118
-43

So 118₁₀ is 0111 0110₂

and 43₁₀ is 0010 0111₂ and it's complement (inverse is 1101 1000₁)

Now, add the two binary words:

  0111 0110
+1101 1000
  0100 1110 and now add 1
+0000 0001
  0100 1011

With these two printed examples, now you can work a little on your worksheet. If you need to review, you can use the above information, or you can visit this tutorial (from which much of this content is drawn)

 

In class, you will have a worksheet to help you master this concept of signed numbers.

Homework